Optics of Intraocular Lenses
Introduction
The implantation of intraocular lenses (IOLs) following removal of a cataractous crystalline lens is one of the most common surgical procedures performed in the United States. From an optical standpoint, the typical goal of the implant is to provide optical power in conjunction with the cornea to focus light from a distant object onto the retina. Prior to implantation of the lens, the surgeon must predict what lens power is necessary to provide appropriate distance vision. The calculation of the proper lens power depends on individual patient factors such as corneal power, axial length, anterior chamber depth, and the final position of the IOL in the eye. Although the majority of lens implantations are for distance correction only and cannot correct for astigmatism, newer technologies offer the potential for cylinder error correction and for simultaneous correction of near and distance vision.
Optics of an IOL
The total optical power of the emmetropic eye is approximately 60 D, of which the corneal power comprises approximately two-thirds of the power. The crystalline lenses, therefore, must provide the balance of power to achieve sharp imaging on the retina. When opacities appear in the crystalline lens that cause significant visual deficits, the crystalline lens is removed and replaced by an IOL. The power of the IOL must replace the power originally provided by the crystalline and also account for any preoperative spherical refractive error. Due to anatomical variations in the population such as differences in eye length, corneal curvature (which affects corneal power), and refractive error, values for IOL powers vary over a broad range. Typical range of powers for IOLs is 5 D to 30 D in steps of 0.5 D for the most common lenses in the range. Additional IOL lens powers exist for cases of extreme refractive error or axial length.
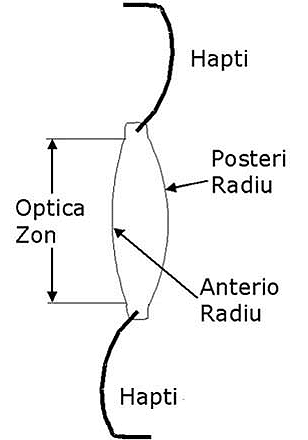
IOLs come in a variety of shapes and sizes. Slide 1 shows a generic layout for an IOL. The lens itself is made up of a transparent polymer material such as PMMA, silicone, or acrylic. The material may also be designed to absorb ultraviolet light. The anterior and posterior surfaces of the lens will each have a radius of curvature designed to refract light as it passes from aqueous to lens and again to aqueous. Variations on the relationship between the radii of curvature of the front and back surfaces of the lens exist. Biconvex lenses have two different radii of curvature for the surfaces, whereas equiconvex lenses have the same radius of curvature on both surfaces. Planoconvex lenses have one flat surface and the second surface has a radius of curvature. The aperture of these refracting surfaces defines the optical zone or region of the IOL.
|
Haptics connected to the edge of the IOL are used to fixate the lens in the eye. The two most common haptic designs are a modified-C design, as seen in Slide 1, and a plate haptic, which is a solid flange of material that comes off the edge of the lens. The lenses may have a narrow non-optical band around the outside of the lens used to connect the haptic to the lens. The haptics may be at an angle relative to the lens to vault the lens relative to the point in the eye where the lens is fixated. The specific haptic design controls where and how the lens sits in the eye.
IOL Power Calculations
Because direct measurements of the power of the crystalline lens in the eye cannot be easily made, the crystalline lens power must be inferred from different clinical measures. The IOL power appropriate for a patient is then chosen based on these clinical measures. Two different techniques have been used to determine the IOL power for implantation. The first technique is based on regression analysis and the second technique uses theoretical models of the eye as its foundation.
Perhaps the most famous and widely used regression formulas are the Sanders, Retzlaff, and Kraff (SRK) and SRK II formulas.1-4 The developers of these formulas originally examined the outcomes of a large series of IOL implants and used regression analysis to determine the relationship between emmetropic IOL power (P), axial length (L), and average keratometry (K). They found the simple relationship:
P = A - 0.9K - 2.5L (1)
where A is a constant that depends on the specifics of the IOL design. Lens manufacturers suggest a value for the A-constant for each of their lenses, and recommend that surgeons personalize their A-constants to account for variations in surgical technique. Suggested A-constants typically range from 116.9 to 119. The simplicity of the SRK formula and its accuracy in the majority of cases has led to its widespread use. The original formula, however, is inaccurate for extremely long or extremely short eyes. The developers have made adjustments to the A-constant based on the value of L to account for these extreme cases. This adjusted formulation is now known as the SRK II formula.4
Theoretical IOL power formulas,5-6 while offering more flexibility to handle individual variations and odd cases, have not gained wide acceptance mainly because of their apparent complexity. However, the foundation of these types of formulas is in geometrical optics, and they should not be ignored. The theoretical formulas all stem from a simple relationship of determining the total power (Ptotal) of two lenses with powers P1 and P2, separated in space by a distance (t) and an index of refraction (n). This relationship is given by:
Ptotal = P1 + P2 - (t/n) P1 x P2 (2)
In the case of IOL implantation, Ptotal is the total power on the presurgical eye plus the spherical equivalent refractive error. P1 is the power of the cornea, P2 is the power of the IOL, t is the separation between the rear principal plane of the cornea and the front principal plane of the IOL, and n is the index of refraction of the aqueous humor. Of course this equation can be rearranged to solve for P2, the power of the IOL, such that:
P2 = (Ptotal - P1) / (1 - (t/n)P1) (3)
So the unknowns in finding the IOL power are Ptotal, P1, t, and n. The index of refraction (n) of the aqueous humor is 1.336. The complexity in theoretical formulas arises in the choices for Ptotal, P1, and t. Ptotal is related to the axial length of the eye, the optical thickness of the retina, and the vertex-adjusted spherical equivalent refractive error. The assumptions made in calculating Ptotal include the speed of sound in the various materials of the eye, which affects the ultrasonic measurement of axial length, the distance of the photoreceptors from the surface of the retina, and the vertex distance from the spectacle to the corneal plane. Poor assumptions in any of these values can lead to errors in IOL powers. P1 is the total optical power of the cornea and depends on the radii of curvature of both the anterior and posterior corneal surfaces. P1 is usually obtained from keratometry, which physically measures the radius of curvature of the anterior cornea and makes assumptions as to the optical effect of the posterior cornea. Again, poor assumptions on the effect of the posterior cornea can lead to errors in IOL power. Finally, the separation (t) between the cornea and the yet to be implanted IOL must be assumed. Holladay5 defines t as the anterior chamber depth plus a "surgeon factor," that is, the position of the IOL relative to the iris plane. He also shows a relationship between the surgeon factor and the A-constant from above. Therefore, the A-constant is related to the position of the IOL within the eye. Errors in the assumed position of the IOL in the eye can also lead to errors in the calculation of IOL power.
The theoretical formulas, although more complex than the regression formulas, offer flexibility in situations where the patient may have an out of the ordinary anterior chamber depth or axial length. Theoretical formulas can also account for differences in ultrasonic measurement devices. These formulas should be used in situations where uncommon or irregular measures of the eye appear.
Side Effects
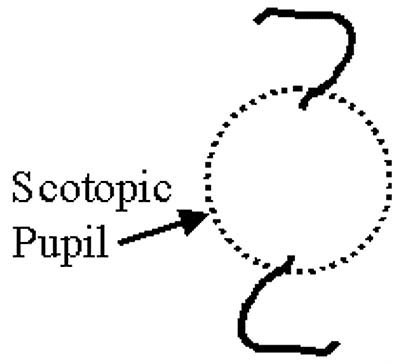
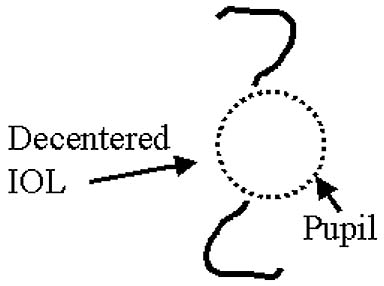
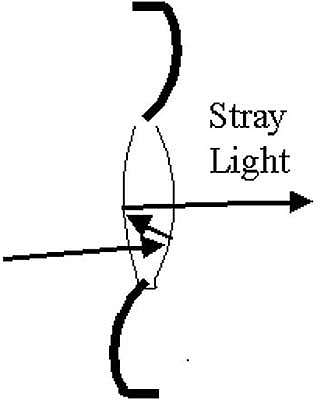
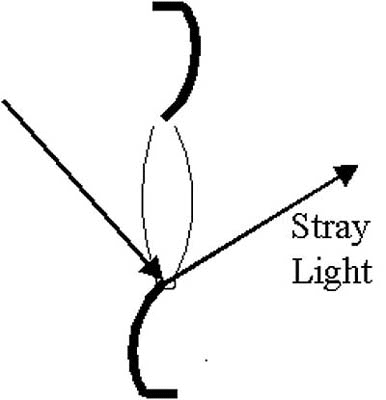
Optical side effects appear with the implantation of IOLs. These effects take the form of halos, crescents, and glare. Slides 2A to 2D summarize the mechanisms for introducing stray light into the field of vision of the pseudophakic patient. Halos can appear around bright lights if the scotopic pupil gets larger than the diameter of the optical zone of the IOL (Slide 2A). Light entering the periphery of the pupil is only refracted by the cornea and not the IOL, and, therefore, not focused at the retina, but instead well behind the retina. A similar side effect occurs if the IOL is decentered with regard to the pupil (Slide 2B). Too large of a decentration will cause an aphakic crescent region to appear and consequently, the perception of crescents for the patient. Larger optical zones and good placement of the lens help to minimize the risk of halos and crescents. Glare can appear as stray light in the eye washes over the foveal vision. Glare can be caused by retroreflections off the surfaces of the IOL (Slide 2C) and by reflections off the edge of the IOL (Slide 2D). Many manufacturers have redesigned the edges of IOLs to help eliminate glare problems.
|
|
|
|
Effects of Refractive Surgery
In examining the theoretical formulas for determining IOL power, a series of assumptions were made about the properties of the eye. Errors in calculating IOL power can arise from a breakdown in any of these assumptions. Refractive surgeries such as radial keratotomy (RK), photorefractive keratectomy (PRK), and laser in situ keratomileusis (LASIK) can cause a breakdown in the measurement of the corneal power or K values. First, all of these procedures change the shape of the anterior cornea, making it a complex-shaped surface. This complexity distorts keratometry, which measures corneal power by assuming the corneal front surface is spherical. This assumption is poor in post-refractive surgery patients. Secondly, these surgeries change the relationship between the shape of the anterior cornea and the posterior cornea, thus breaking down the assumptions of keratometry as a measure of total corneal power.
Koch and colleagues7 have suggested three techniques for adjusting the K values used in determining IOL power in post-refractive surgery patients. First, if the information is available, the post-refractive surgery K values are determined by subtracting the change in refractive error caused by the refractive surgery from the pre-refractive surgery K values. This technique has the drawback that the pre-refractive surgery information may not be readily available. The second technique involves performing a contact lens overrefraction, but has a drawback in that it requires the patient to have adequate visual acuity to obtain a good manifest refraction. Finally, computerized videokeratography can be used to measure the K values. Celikkol and colleagues8 found that by averaging the third ring on a Tomey TMS-1 videokeratograph, better estimates of corneal power were achieved. Surgeons attempting cataract surgery on post-refractive surgery patients should be aware of the possible errors and the techniques for reducing their effect.
Toric IOLs
Most IOL designs are rotationally symmetric, meaning that they can only correct for spherical refractive error in the eye. Surgeons may perform astigmatic keratectomy (AK) to reduce residual astigmatism in their patients. However, toric IOLs may offer an alternative to AK. Toric IOLs have different powers along different meridians and can therefore correct for cylinder error. Two potential difficulties arise with toric IOLs. First, accurate alignment and fixation of the lens is required. The axis of the IOL must be aligned with the axis of the cylinder error or a reduced correction will be seen. Also, the rotational alignment must remain fixed following surgery, so any postsurgical rotation of the lens would degrade correction and can even introduce additional cylinder error if the rotation was large enough. The second difficulty with toric IOLs occurs if significant lenticular astigmatism exists in conjunction with corneal astigmatism. Upon removal of the astigmatic crystalline lens, the toric IOL must be aligned with the corneal astigmatism. This axis of alignment may be rotated relative to the axis of the manifest refraction.
Multifocal IOLs
Multifocal IOLs are used in an attempt to simultaneously provide good distance and near vision in a pseudophakic patient. Various designs have been tried to achieve this multifocality, but the designs fall into two categories: refractive multifocal and diffractive multifocal. Refractive multifocals typically have a series of concentric zones with different optical powers. For example, the center and an annular region in the periphery of a multifocal IOL may have a power appropriate to correct for distance vision in a patient. In between these two zones is a region of higher optical power (an "add" power) that is appropriate for near vision. Implantation of these types of lenses produces two simultaneous images to be formed on the retina of the patient. One image has distant objects in focus and near objects out of focus, and the second image has distant objects out of focus and near objects in focus. It is up to the patient to accept the in-focus portions of both images and ignore the out-of-focus portions. Typically, these patients show losses in contrast sensitivity for distance vision, in exchange for improved near vision. Modulation of the number and dimensions of the near and distance zones in refractive IOLs has been performed by manufacturers in an attempt to optimize the performance of these lenses.
Diffractive IOLs take advantage of diffraction caused by small, closely spaced, annular grooves cut into the lens surface. The diffraction causes an infinite number of foci for the lens, but most of the power goes into the first two foci. By adjusting the spacing and shape of the grooves, the optical properties of the diffractive IOL can be adjusted to be suitable for a multifocal lens. These IOLs are associated with similar problems as refractive multifocal IOLs.
Accommodating IOLs
An advance in technology includes accommodating IOLs. These IOLs provide good distance, intermediate, and near vision by allowing the lens to shift position in the eye to adjust focus. This technology is based on the assumption that the ciliary muscle in older adults still functions properly, but the crystalline lens has become too stiff or large to accommodate properly. The new IOLs are designed with haptics that will cause the lens to move back and forth in the eye as the ciliary muscle puts pressure on the haptics. Several IOL designs of this type are currently in clinical trials and their success or failure is not yet known.
Light-Adjustable IOLs
Another emerging technology is light-adjustable IOLs. These lenses are made with a material that can change shape if exposed to ultraviolet light. The concept behind these lenses is to implant a lens that is close to the ideal power, and then adjust the lens power with ultraviolet light following the cataract procedure and appropriate healing. Once the lens has been adjusted to the proper power, it is "fixed" so that additional ultraviolet exposure cannot change the shape of the lens. This technology may also be able to correct for astigmatic errors and even aberrations in the eye.
References
- Retzlaff J. A new intraocular lens calculation formula. Am Intra-Ocular Implant Soc J. 1980;6:148-152.
- Sanders DR, Kraff MC. Improvement of intraocular lens power calculation using empirical data. Am Intra-Ocular Implant Soc J. 1980;6:263-267.
- Retzlaff J. Posterior chamber implant power calculation regression formulas. Am Intra-Ocular Implant Soc J. 1980;6:268-270.
- Sanders DR, Retzlaff J, Kraff MC. Comparison of the SRK II formula and other second-generation formulas. J Cataract Refract Surg. 1988;14:136-141.
- Holladay JT, Musgrove KH, Prager TC, Lewis JW, Chandler TY, Ruiz RS. A three-part system for refining intraocular lens power calculations. J Cataract Refract Surg. 1988;14:17-23.
- Retzlaff J, Sanders DR, Kraff MC. Development of the SRK/T intraocular lens implant power calculation formula. J Cataract Refract Surg. 1990;16:333-340.
- Koch DD, Liu JF, Hyde LL, Rock RL, Emery JM. Refractive complications of cataract surgery after radial keratotomy. Am J Ophthalmol. 1989;108:676-682.
- Celikkol L, Pavlopoulos G, Weinstein B, Celikkol G, Feldman ST. Calculation of intraocular lens power after radial keratotomy with computerized videokeratography. Am J Ophthalmol. 1995;120:739-750.