Size of phaco needle affects flow rate

Issue: October 2007

One of my highly intelligent residents recently inquired about my personal fluidic settings for our phaco machine platform. I told him the numbers: maximum vacuum of 250 mm Hg, flow rate of 45 cc/min and 90-cm bottle height. But I told him that the numbers don’t mean much without knowing the specific phaco needle being used. He seemed confused.

Uday Devgan

The flow of milkshakes

I brought up the example of a milkshake: If you drink the milkshake with a small-caliber cocktail straw, then you’ll need much higher vacuum and you’ll likely achieve a low flow rate (Figure 1a). But, if a larger-bore straw is used then the vacuum needed is much less and a higher flow rate can be achieved, resulting in more efficient aspiration of the shake (Figure 1b). With that example, he immediately understood the concept and replied, “Right, Poiseuille’s equation for vascular blood flow – it’s related to the radius of the vessel to the fourth power.”

Poiseuille’s equation

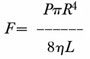F = flow; P= pressure gradient;
R= radius of the tube;
ç = viscosity of fluid; L = length of the tube

Poiseuille’s law is even more applicable to our phaco machines than it is to blood flow because we are using a Newtonian fluid (water/balanced salt solution) and long straight tubes (low compliance phaco machine tubing) with relatively laminar flow, instead of blood flowing through convoluted vessels in a pulsatile manner.

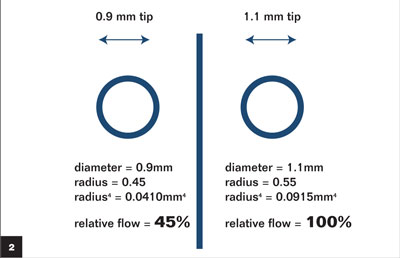
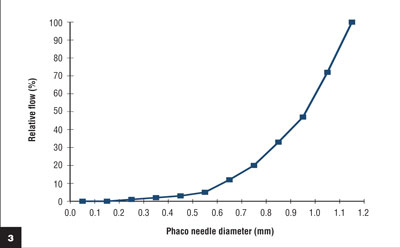
The important thing to remember from Poiseuille’s equation is that the flow is proportional to the radius of the tube to the fourth power. This means that a small change in the size of the phaco needle can result in a large change in the flow (Figure 2). Comparing two common size phaco needles, 0.9 mm vs. 1.1 mm, with all other factors equal, it is surprising to see that the flow through the larger 1.1-mm needle is more than twice that of the 0.9-mm needle. As the needle size decreases, the flow drops exponentially (Figure 3).

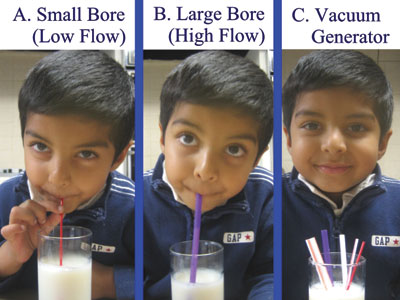The Milkshake Analogy: (a) A cocktail straw has a small bore and therefore less flow, necessitating the use of higher vacuum in the mouth to generate flow. (b) A larger bore straw allows for higher flow with the use of lower vacuum levels in the mouth. (c) The vacuum generator used for this study.

Images: Devgan U

Changing phaco needles

If we switch from a 1.1-mm phaco needle to a 0.9-mm needle, with all other phaco parameters unchanged, the relative flow will decrease by more than half to 45% of the relative flow through the 1.1-mm needle. In order to achieve the same flow while decreasing the needle size, a substantial increase in the pressure gradient (P from Poiseuille’s equation) is required.

Things are further complicated if a phaco needle with an additional hole in its sidewall is used, such as those that are intended to maintain low flow during times of complete occlusion. Poiseuille’s equation and the milkshake analogy still apply, albeit this time with a straw with a small hole in its side. During states of higher flow and lower vacuum, the flow through the additional bypass hole is limited. However, when there is occlusion of the end of the needle, the vacuum increases dramatically and the flow through the end of the needle drops; therefore, the flow through the bypass hole increases. As compared to a traditional phaco needle, higher phaco machine vacuum levels would be required to achieve the same holding power at the phaco tip.

Applications

As shown in Figure 3, there is a lower limit when it comes to phaco needle size – we need to balance the efficiency of surgery (which is better with larger bores) with the benefits of smaller incisions (which better accommodate smaller bores).

When doing bimanual cataract surgery with the infusion through an irrigating chopper, Poiseuille’s equation applies to this infusion flow. I have compared flow rates of 19-, 20-, and 21-gauge irrigating choppers, and the difference is significant. Bimanual surgeons compensate for this decrease in flow by increasing the pressure gradient (P) via raising the infusion bottle to its maximum height or even further by using forced infusion.

If you plan on using new irrigating instruments, measuring their flow outside the eye (in cc per minute) with your bottle height setting prior to surgery is helpful. You can then set your phaco machine flow rate at a lower level than the infusion flow rate in order to maintain chamber stability.

The take-home message

There’s no need to memorize Poiseuille’s equation, but it is critical to remember that the size of our instruments affects their flow rates in an exponential manner. When in doubt, just think of milkshakes.

Figure 2: The important thing to remember from Poiseuille’s equation is that the flow is proportional to the radius of the tube to the fourth power
The important thing to remember from Poiseuille’s equation is that the flow is proportional to the radius of the tube to the fourth power. This means that a small change in the size of the phaco needle can result in a large change in the flow.

Figure 3: As the needle size decreases, the flow drops exponentially
As the needle size decreases, the flow drops exponentially.

For Your Information:

Uday Devgan, MD, FACS, is an assistant clinical professor at the Jules Stein Eye Institute at the University of California, Los Angeles, and in private practice in Sun Valley, Calif. He can be reached at 9375 San Fernando Road, Sun Valley, CA 91352; 818-768-3000; fax: 818-504-4463; e-mail: devgan@ucla.edu.