Learning a new language: understanding the terminology of wavefront-guided ablation

In the second part of our series, we describe some of the concepts and the basic terminology behind the next generation of refractive diagnostics.

With the growth of interest in wavefront-guided ablation for refractive surgery, many ophthalmologists are struggling to grasp the concepts that describe this new technology.

Clinicians are bombarded with scientific literature and podium presentations touting the results of wavefront-guided refractive surgery. They hear terms tossed around such as Zernike polynomials, higher-order aberrations, root mean square, point spread function. And they are left with one overwhelming question: What does it all mean?

"Wavefront technology is a new diagnostic tool. Just like topography devices previously, it needs to be submerged into the mainstream for a while before surgeons begin to the hang of it," said Jack T. Holladay, MD, MSEE, FACS a refractive surgeon and clinical professor of ophthalmology at Baylor College of Medicine.

"For wavefront technology in particular, there has been resistance to learn it because the fundamentals do not utilize measurements that ophthalmologists are familiar with. It’s a whole new ball game," said Dr. Holladay in a recent interview with Ocular Surgery News.

For part two of our series on customized ablation, we concentrate on the basic definitions and components of this new diagnostic technology, in an effort to fill in the blanks for those to whom the technology is new — in other words, for all of us.

Irregular wavefronts

In simplest terms, a wavefront-guided LASIK system consists of two parts, a wavefront sensor and an excimer laser that is programmed based on information from the sensor. The wavefront sensor system includes a fixation target, an input laser beam that generates a point light source, a wavefront sensor that measures the slope of the exiting wavefront, and software that will determine the characteristics of the excimer ablation.

The visual fixation target assists the patient in maintaining view, direction and accommodation during the wavefront measurement. While the patient fixates, a laser beam is shined into the eye.

"The input laser beam generates a point-light source onto the retina. The light is reflected from the retina back through the pupil, and the wavefront of the light leaving the pupil is relayed to the wavefront sensor," said Junzhong Liang, PhD, a physicist who has participated in the development of wavefront technology in ophthalmology.

"The wavefront gets distorted by inhomogeneities in the refractive properties in the refractive media of the human eye," explained Josef F. Bille, PhD, of the University of Heidelberg in Germany. Dr. Bille is an optical physicist and a pioneer of wavefront technology for ophthalmology.

When the laser beam enters the eye, it has a flat wavefront. In theory, a perfect human eye would reflect back a beam with its wavefront still flat. But in a normal human eye — after the beam of light has traveled through an imperfect crystalline lens, an irregular cornea and the other ocular media — the flat wavefront has become irregular. Analysis of its aberrations can reveal the aberrations of the human optical system it has just traveled through.

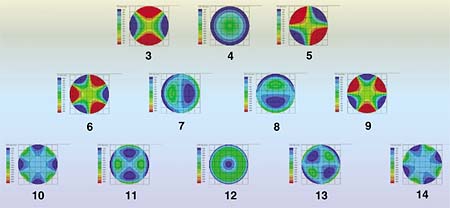
Higher-order aberrations: wavefront shapes Each Zernike polynomial describes a certain type of surface. The second-order aberrations correspond to the conventional refractive errors, defocus and astigmatism. The higher-order polynomials describe more complex shapes such as trefoil (wavefront shapes with threefold symmetry) and quadrefoil (wavefront shapes with fourfold symmetry). Figure courtesy of Michael Mrochen, PhD.

Zernike blueprints

The wavefront errors of the eye’s optical system are registered by a wavefront sensor, and software analyzes the results.

"The wavefront sensor measures the slopes of the wavefront across the pupil of the eye using the Hartmann-Shack sensor," Dr. Liang said. "Then the software reconstructs the wavefront map using a least-squares fit with the Zernike polynomials. Zernike decomposition is one of the methods used to convert the measurements."

Conventional LASIK can correct two types of error on the cornea — spherical and cylindrical. The promise of wavefront-guided refractive surgery is to create treatments tailored to the individual eye based on the total wavefront error in patients’ eyes rather than the conventional manifest refraction, he said.

Zernike polynomials are used as the mathematical blueprints of ocular aberrations.

Each Zernike polynomial, called a mode, describes a certain type of shape, a certain three-dimensional surface. The second-order Zernike terms represent the conventional aberrations

defocus (spherical correction) and astigmatism. Zernike aberrations above the second order are called high-order aberrations. The third-order Zernike terms are coma and trefoil (a wavefront shape with threefold symmetry). The fourth order Zernike terms include spherical aberration and four other terms, and so on.

The Zernike polynomials are an infinite set, but in ophthalmology discussion has generally been limited to the first 15 or so.

Dr. Liang explained: "For spherical aberration, for instance, instead of describing the wavefront error across the pupil, you can use one number, and that one number is associated with a specific shape. If you have a lot of modes and you put them together, they can give you any shape you would like to represent. This is called the decomposition.

"The reason we do decomposition is twofold," he continued. "First is to correlate to the aberrations we know. The second is, for normal eyes, we can use much fewer coefficients to represent the same wavefront shape. Typically you have many fewer modes than the number of measurements across the pupil."

Importance of pupil size

According to Michael Mrochen, PhD, of the Swiss Federal Institute of Technology in Zurich, Switzerland, more than 40% of "normal" eyes have higher order aberrations that are 0.25 D or higher if the pupil size is increased from 3 mm to 6 mm in diameter.

"These optical aberrations of higher orders can alter the spherocylindrical data by several diopters," Dr. Mrochen said recently at the meeting of the American Academy of Ophthalmology.

He said refraction data can only be compared at the same pupil size. Determining the refraction of a patient at a pupil size of 3 mm to 4 mm and then using a 6 mm or 7 mm optical zone will lead to unnecessary tissue removal. He said wavefront-guided treatments are the solution for that problem.

Processing wavefront data

While truly understanding the particulars of Zernike decomposition may not be essential to the operating surgeon, it is integral to the measurement capabilities of the sensor.

"By using this information, aberrometer software can plot the ocular aberrations on a graph and create a wavefront map. The map is imaged on the display screen for physician evaluation," Dr. Liang said.

"Surgeons should not be intimidated by this map," Dr. Holladay said. "All they need to know is that this map is just like a topography map. The knowledge needed for evaluating what is presented in front of us is virtually the same. "

Alongside the wavefront map, surgeons are given information in two additional ways: through conventional refraction in diopters, and in Zernike form.

"Once you are given a description of the aberrations, you can compute the image blur of a point object, like a star, called point-spread function of the eye," Dr. Liang said. "This added information will help you to understand what the quality of their visual performance is — how well patients are imaging objects."

Once surgeons have interpreted the two-dimensional map and the additional data presented, they can use this information to program a laser to perform customized ablation.

Microns to diopters

If surgeons choose to perform LASIK surgery, they can decide how much tissue to ablate by using simple math, Dr. Holladay said.

"Surgeons can add the deviation to the corneal thickness and decide how many laser pulses — at 0.2 µm per pulse — need to be delivered to the imperfect areas of the cornea," Dr. Holladay said.

"It is easy to decide how much tissue to ablate with the excimer laser once you know the total wavefront map, just like the conventional aberrations of astigmatism and defocus, because there is a 1-to-1 relationship between refraction diopter and wavefront map in micron values," Dr. Liang said. "The aberrometer will calculate the conversion for you."

However, when higher-order aberrations come into play, the conversion becomes more difficult, Dr. Holladay said.

"Once surgeons are presented with higher-order aberrations, the calculations become much more complex," Dr. Holladay said. In general, converting microns to diopters has been difficult for ophthalmologists because most of them are trained to analyze refractive errors in diopter values, not micron values.

"So," he said, "it’s a problem for ophthalmologists who have learned in diopters for the last 20 years. Now, they have to throw away everything that they learned and start thinking in microns."

For this reason, he speculates that many surgeons may be slow to adopt wavefront technology.

Dr. Holladay suggests that surgeons strictly look at the wavefront map for a true representation when analyzing errors.

"Just like topography, the map will guide them," he added.

Laser ablation

The wavefront sensor delivers the refractive error information, or a treatment table, to the excimer laser.

"When the excimer laser receives the information in Zernike form, it generates a treatment table using special algorithms," Dr. Liang said.

"Based on the beam characteristics — energy per pulse, repetition rate, pulse size and pulse shape — and many other factors, the special algorithms generate a treatment table that defines the location, size and sequence of each pulse of ultraviolet light in order to ablate a corneal defect," Dr. Liang explained.

Not all excimer laser algorithms are created equal.

"Different brands of lasers have different calculation methods for their algorithms. So the quality of correction is slightly different for each laser," he said.

Laser ablation corrects the targeted areas in the manner specified by the software. Ideally, the cornea is reshaped to a form that leads to optimal visual performance.

Induces less aberration

Wavefront-guided LASIK is said to induce fewer aberrations than standard LASIK, which corrects only defocus and astigmatism.

"Wavefront-guided LASIK induces fewer errors than standard LASIK because it induces less spherical aberration than standard LASIK," Dr. Holladay said. "So it’s less detrimental to the patients’ optical system."

However, optical aberrations will still be present in both types of patients, because laser ablation always induces new errors, he added.

"Since science does not know what the absolute ideal measurements of a perfect visual system are, we unknowingly induce aberrations each time we ablate the cornea," Dr. Holladay said.

"These aberrations exist because surgeons operate on assumptions about what perfect eye qualities are," Dr. Mrochen said. "Right now, we don’t know what the perfect optical system looks like. Until scientists and ophthalmologists get a better understanding of the dynamic characteristics of the human eye, technology-induced aberrations will always exist.

"However, for now, with wavefront technology we have an extremely sophisticated system. So, we can still correct the most important types of aberrations and leave the patient with a more accurate picture of the world," Dr. Mrochen said.

Glossary of Terms
Aberrometer	An optical instrument that measures the total wave aberrations of the eye, beyond the conventional spherocylindrical refractive correction.
Actuator	Active repositioning elements that perform surface displacement or deformation in a deformable mirror.
Adaptive optics	Optical assemblies or components whose performance is monitored with a wavefront sensor and controlled so as to compensate for the aberrations by a wavefront compensator.
Deformable mirror	Mirror that has an actively controlled reflective surface.
Eye’s optics	The refraction system of the eye, consisting of cornea, aqueous humor, crystalline lens and vitreous humor.
Fixation target	A visual target that helps patients maintain the view direction and the accommodation of the eye in ophthalmic instruments.
Modulation transfer function	The ratio of the modulation in the image to that in the original object as a function of spatial frequency (cycles per degree) of the sine wave pattern.
Point-spread function	Energy distribution of light associated with the image of a perfect point (infinitesimal) object.
Root mean square	The integrated root mean square of the differences between the wavefront surface and the mean value of the surface.
Skew ray	Any ray through an optical system that is not a meridional ray. The plane created by a refracted skew ray does not contain the optical axis.
Treatment table	A treatment protocol containing sequence, location, and description of the treatment beam.
Trefoil	Wavefront shape with threefold symmetry.
Wavefront	A surface connecting all field points of the electromagnetic wave that are equidistant from a light source.
Wavefront decomposition	Expansion of a general wavefront function in terms of a function set of polynomials.
Zernike polynomial	An complete set of polynomials, introduced by F. Zernike, that are orthogonal over the interior of a unit circle. Conventional aberrations such as defocus, astigmatism, coma, spherical aberration correlate to a subset of the Zernike polynomials.
Glossary of terms is courtesy of Junzhong Liang, PhD.

For Your Information:

• Josef F. Bille, PhD, can be reached at the Institute of Physics at the University of Heidelberg, Im Neuenheimer Feld 227, D-69120, Heidelberg, Germany; +(49) 6221-549251; fax: +(49) 6221-549839; e-mail: josef.bille@urz.uni-heidelberg.de.
• Junzhong Liang, PhD, principal optical engineer at Visx, can be reached at 3400 Central Expressway, Santa Clara, CA 95051-7122 U.S.A.; +(1) 408-773-7043; fax: +(1) 408-773-7253; e-mail: junzhonl@visx.com.
• Jack T. Holladay, MD, MSEE, FACS can be reached at 5420 Dashwood St., Suite 207, Houston, TX 77081 U.S.A.; +(1) 713-668-7337; +(1) 713-668-7336; e-mail: docholladay@docholladay.com.
• Michael Mrochen, PhD, can be reached at University of Zurich, Department of Ophthalmology Frauenklinik Str. 24 CH - 8091 Zürich Switzerland; +(41) 1-255-4993; fax: +(41) 1-255-4472; e-mail: michael.mrochen@aug.usz.ch.